Correcting a Newtonian

Part of the reason that contrast is so bad on my Newtonian is that it has flare. The other reason is that it is uncorrected. Let's see what it takes to correct the thing.

The mirror is a 300 mm diameter diffraction-limited 1/4 wave parabolic mirror. Sounds awesome, especially the diffraction limited part. When viewing 550 nm (green) light, a 300 mm aperture scope should resolve 1.22*wavelength/diameter = 2.2 microradians. With a 1500 mm focal length, those details are 3.4 microns across on the image plane. My Canon 40D has 5.7 micron pixels, which isn't quite going to catch the details.

Sadly, it turns out that even a perfect parabola produces just a single perfectly focussed dot in the center of the image, and resolution goes downhill out from there. One way to measure resolution is to measure the amount of contrast transmitted by the lens at a particular spatial frequency. We could measure transmission at the diffraction-limited spatial frequency (227 line pairs/mm), but we don't need it to be that good. A more useful frequency is the maximum spatial frequency that the camera supports. The pixels themselves sample 87.7 lp/mm. Because the camera has a Bayer filter to sample colors, it has an antialiasing filter, and the maximum frequency it can sample correctly is a factor of 1.8 smaller, about 48.7 lp/mm.

Here's a graph of the contrast you'd expect to transfer, at both 227 lp/mm (diffraction limit) and 48.7 lp/mm (Canon 40D limit). You can see that resolution from a simple parabolic mirror is only good within a small image circle around the center, and there is almost no contrast available at the diffraction limit.

Once contrast drops to zero, there is no detail left at that frequency. Lower spatial frequencies, corresponding to less detailed imagery, will have contrast at larger and larger radii, and so the picture will look more blurry as you get farther from the center. For photographic lenses, I like to see MTF at the maximum camera frequency of something like 30-40% across the whole field, although I'm willing to accept some dropoff at the corners.

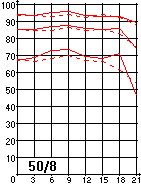Compare the parabolic mirror graph to a similar graph for the Canon 50mm/1.4 lens, in particular, looking at the 40 lp/mm line (the bottom pair). 60-70% MTF. That's a good lens. (I got this graph from photodo.com, which has great data on hundreds of lenses.)

The graphs aren't perfectly comparable, but they're close. The Canon here is stopped down to f/8, which vignettes away the least corrected portion of the aperture. But it performs nearly as well at f/5. Also, this graph is at 40 lp/mm, which is a little easier than the 48.7 lp/mm I'm using to judge the Newtonian. One other detail: in both graphs, there are two lines, one dashed (tangential) and one solid (saggital). Saggital means "in the direction towards and away from the image center", and tangential means"along a curve centered at the image center".

So the reflector looks terrible, but there is hope. Al Nagler at Tele Vue has designed a corrector lens (the Paracorr) that, when combined with a parabolic mirror, gives a well corrected image. I don't have the Paracorr's prescription (I checked the U.S. Patent Office, and found Al's eyepiece patents but no patent for the Paracorr), but I know the basic idea, so I was able to slap something together with Zemax to demonstrate.

Here is the overall scheme: light comes in from infinity from the left, bounces off a parabolic mirror at the far right, and then comes back through a negative doublet, followed by a positive doublet, finally arriving at the image sensor at the far left. I've left out the planar secondary miror that reflects the light out the side, but I've left in the obstruction that it causes. The corrector assembly, as shown, sits just outside the main optical tube. The eyepiece would sit on the other side of the image plane.

When comparing this to a photographic lens, it's best to think of the mirror combined with the two doublets as being the "lens". It actually extends the focal length of the telescope a bit. This picture shows rays bouncing off the primary mirror, going through the two doublets, and arriving at the image plane. Because the doublets are so small relative to the mirror and focal length, it's hard to see the detail.

So, here's the detail. I'm quite pleased with how this turned out: the elements are not ridiculously thick, and there is 50 mm of clearance between the last element and the focus plane, good enough to mount a DSLR (44 mm clearance required) if not a T thread mount (55 mm required). The negative doublet is a bit too close to the mirror, in the sense that it would probably sit right at the edge of the main optical tube, when we'd prefer it to be back a bit so that we can baffle the focus tube so that stray light from the front opening of the tube can't speckle off the doublet.

Designing this wasn't too hard. I left Zemax running overnight doing a global search for an optimum, with no constraints on the glass choice. A real optical designer has more constraints to deal with.

And here's the resulting MTF, polychromatic, no less! This is pretty incredible, I doubt the real Paracorr is this good. It's slightly better, all the way across the field, than the Canon 50mm/1.4. That's astonishing, given that this thing has 7 surfaces (one aspheric -- the mirror) with which to bend the light, compared to 13 in the Canon refractor. Or, compare this to the plot at the top of the post for the performance of the parabolic mirror alone. Night and day.

I think the bottom line is that a Paracorr is a necessary part of a Newtonian telescope, unless it's only used at very high magnifications. Unsurprisingly, the Paracorr is the best-selling product made by Al Nagler's company.